位运算技巧

1. 判断奇偶

if (x & 1 == 0) {  // 7   ... 0111 & 1 == ... 0001
    // 偶数
} else {
    // 奇数
}

2. 高位清零、翻转

如想将一个数只保留最后四位。则让他与仅后四位为1的数字做与运算。 如下，留下来的就是x的后四位

x & 15 // x &  ...0000 1111

那同样，将一个数后四位设为1就是用或运算。如下

x | 15 // x | ...0000 1111

那同样，翻转一个数的某几位就是用异或运算（相同为0，相异为1）。如下

x ^ 15 // x ^ ...0000 1111

针对情况与，还有个小技巧。如果想让一个数后几位清零。可以使用取反运算符。因为取反优先级更高。

x & ~15 // x & 1111... 1111 0000

3. 交换两个数

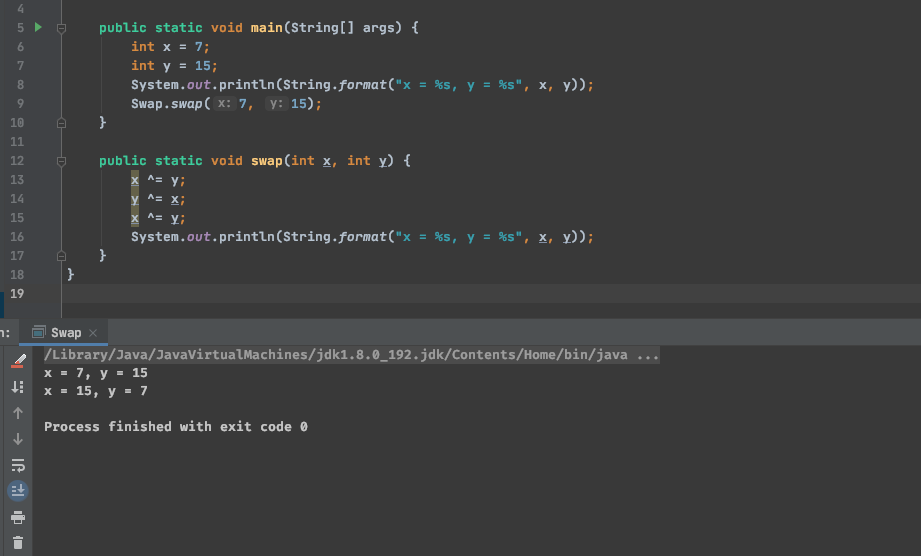
借用异或将两个数进行交换，是一个经典中的经典。如下

public void swap(int x, int y) {
        x ^= y;
        y ^= x;
        x ^= y;
}

4. 位移说明

因为计算机用补码运算，所以正数无论是有符号、无符号位移结果都一致。

1. << x 左移

将一个数的二进制左移x位，末位用0填充。在移动的位数上1没有溢出到符号位之前，可以视为乘以2的x次方

但如果涉及到符号位变动或高位溢出，则不能视为乘法。如下结果为 -2147483648

1073741824 << 1 // 0100 0000... << 1

2. >> x 右移

将一个数的二进制右移x位，正数高位用0填充，负数用1填充。 正数没到0时可看作除以2的x次方

如下

-10 >> 2 // 1000 0000... 1010 >> 2


1000 0000... 1010 -> 1111 1111... 0101 -> 1111 1111... 0110 (原码到补码)

1111 1111... 1101 (右移2位) -> 1111 1111... 1100 -> 1000 0000... 0011 = -3

3. <<< x 无符号左移

逻辑同左移

4. >>> x 无符号右移

这里和右移有区别，无符号右移无论正负，高位都是拿0填充。

如下 -10经过无符号右移后变成了 1073741821

-10 >>> 2 // 1000 0000... 1010 >>> 2

1000 0000... 1010 -> 1111 1111... 0101 -> 1111 1111... 0110 (到补码)
0011 1111... 1101 -> 0011 1111...